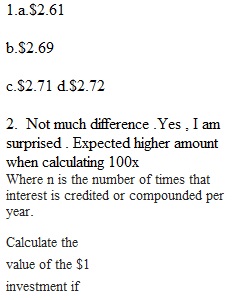
Q Compound Interest Application Imagine you start with $1.00 in a bank account that pays 100% interest per year. If the interest is credited once (annually) at the end of the year, the value of the account at year-end will be $2.00. If the interest is credited twice in the year (semi-annually), the interest rate for each 6 months will be 50% (100%/2), so the initial $1 is multiplied by 1.5 twice (1 to include the original principal and .5 to add 50% more), yielding $1.00×1.52 = $2.25 at the end of the year. Compounding quarterly yields $1.00×1.254 = $2.4414. This formula can be written as: Where n is the number of times that interest is credited or compounded per year. 1. Calculate the value of the $1 investment if the interest is compounded a. Monthly b. Weekly c. Daily d. 1000 times in a year 2. Is there a big different between compounding monthly and 1000 times/year? Is this a surprising result to you? 3. Use a graphing calculator or www.desmos.com/calculator , make a graph of the investment value results you calculated in part (1) and the data given in the top paragraph. As a start, look at a window such as -100<x<1200 and -1<y<4, where x is representing the values for n. Take a screen shot and include it. 3. What is the amount if interest is compounded hourly? 4. What is the amount if n=1,000,000,000? 5. Do you think the value of the $1 investment can grow unbounded (to infinity)? What does your graph suggest? Is there a limit of some sort? If so, what is it?

View Related Questions